Does digits prefer certain positions?

GENERAL CONSIDERATIONS / EXPECTED VALUES

Could it be that on every 53th position in the Pi sequence we will find abnormal many "7"?
Or more general:
Does there exist a favourite distance S, that when stepping thru the Pi data with equal steps of length S we will find "much more" of digit X than of others?
To answer this we have to follow this certain number and analyze the position p of its appearences by the formula F = p mod k. In the example above k=53 and F will last from 0 to 52.
Performing this analysis for all ten digits from 0 to 9 we get k groups of 10 numbers showing the frequency of each number to be found at a "k^th position" with possible additional shift from 0 to k-1.
If Pi is random we should find a distribution of all these groups of ten numbers near to the normal one.

It is quite enough to test p mod k for only prime numbers k, because a regularity in any other number will be reflected in the results for its prim factors.

RESULTS

Here is an example how the detailed result tables look like.

Tested: Position of any Digit 0-9 mod 7
Start. Pos.: 1 
Digits examined: 10¹¹
Expected Average: 1.428.571.428,57
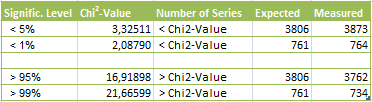
Chi²(95%;f=9) = 16,919

The test was passed for all primes between 2 and 1000, so 76127 series were produced.