Analyzing the DISTANCE of sequences of Length L:
What is the distribution like?

GENERAL CONSIDERATIONS / EXPECTED VALUES

When testing the difference of sums we knew that this test is not very sensitive due to the combinatorical proberty of the sum, generally: n + m = (n-x) + (m+x).

But we can treat any digit position as an coordinate value and ask about the distance of to chains.
Let us define the DISTANCE OF TWO CHAINS (DOC) as:

DOC = SUM _i=1,L ABS(X_i - Y_i)
where
L = length of chains X and Y
X_i,Y_i = i-th digit of chain X respectively Y

Here is an example for Pi with L=5.
First sequence X=14159
First sequence Y=26535
DOC = abs(1-2) + abs(4-6) + abs(1-5) + abs(5-3) + abs(9-5) =
= 1 + 2 + 4 + 2 + 4 = 13

The recursive law for the expected distribution can easily be found.
Let w(L,d) be the probability that two chains of length L have a DOC = d.
Then w(L+1,d) = w(L,d) / 10 + sum w(L,d-i) x 2*(10-i)/100
where sum is taken for i=1 to 9.

Starting condition is:
w(1,d) = 2*(10-d)/100 for d=1-9
w(1,0) = 1/10

We understand that the DOC-value can be an indicator for possible correlations between digits of neighbouring sequences.

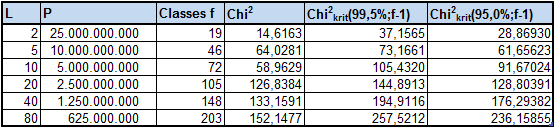
RESULTS

Digits analyzed: N = 100 * 10 ¹¹
DOC-Analysis started at digit: 1

L=Length of Chains; P=Number of exam.Calculations=N / (2xL)
Classes=Number of statist. relevant classes