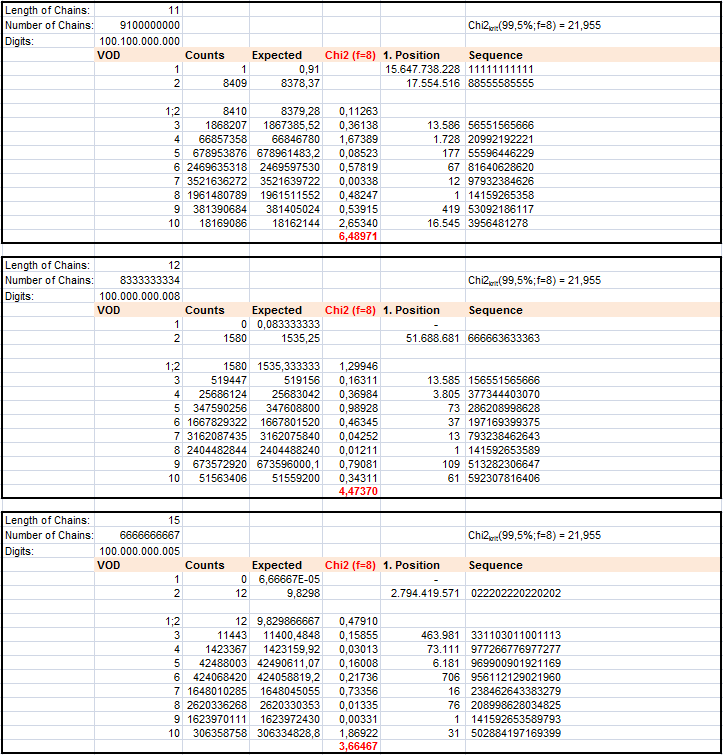
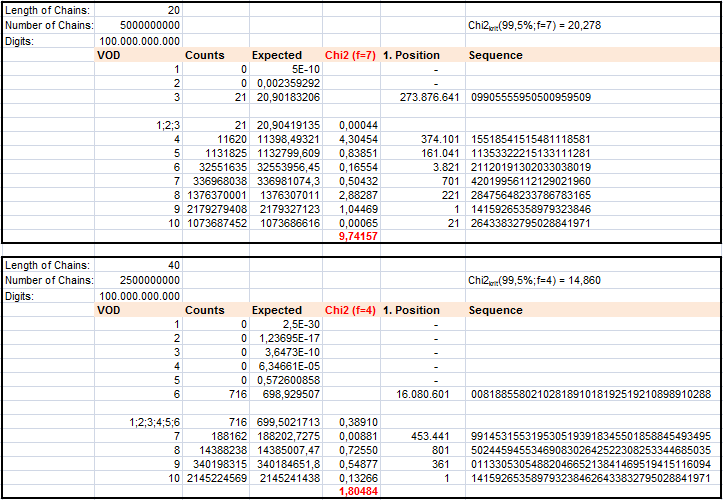
How many DIFFERENT DIGITS are contained in a sequence of length L?

GENERAL CONSIDERATIONS / EXPECTED VALUES

When testing longer chains we gonna start with a simple question:
How many DIFFERENT DIGITS are contained in a chain of length L?
Let us call this number the Variety of digits VOD.

Here is an example for Pi with L=5.
14159 -> VOD = 4 ; 26535 -> VOD = 4 ; 89793 -> VOD = 4 ; 23846 -> VOD = 5
26433 -> VOD = 4 ; 83279 -> VOD = 5 ; 50288 -> VOD = 4;  41971 -> VOD = 4
69399 -> VOD = 3 ; 37510 -> VOD = 5

The construction law for the VOD-distribution is easy to find.
Let w(L,d) be the probability that a chain of length L consists of exactly d different digits.
For L=1 we have even one digit:
w(1,d)=1 for d=1   and   w(1,d)=0 for d>1

For L>1 any w(L,d) can be calculated from its predecessor:
w(L+1,d) = w(L,d) x d/10 + w(L,d-1) x (10-d)/10

Finding a VOD=1 for L=5 is just the same as searching for a single digit run of length 5 (e.g. 11111).
But analyzing single digit runs is limited to L~7 due to the available data.
Thus testing variety of digits up to L=40 is a chance to get a better feeling for the regularity of single digit distribution. More than this the VOD can be an indicator for clusters.

RESULTS